OpenSees 是如何实现的-翰林苑|董翰林的个人网站

OpenSees 是一个主要由 C++ 写成的程序，利用了面向对象的程序设计。除了 C++ 之外，它的一部分求解功能通过 Fortran 和 C 程序来实现。与用户的交互使用 Tcl 语言和 Python 语言来实现。本文我们来了解一下 OpenSees 的核心部分是如何架构起来的。

文件树

OpenSees 的代码目前已经从官网的 svn 托管系统中下线，迁移到了 git 托管系统。在 GitHub 中可以看到 OpenSees 的代码仓库。

先来看代码仓库中的文件树

.
├── COPYRIGHT
├── DEVELOPER
├── EXAMPLES
├── MAKES
├── Makefile
├── OTHER
├── README
├── SCRIPTS
├── SRC
├── Win32
├── Win64
└── Workshops

其中，SRC 是源代码的主要目录。Makefile MAKES Win32 Win64 都是用于编译的。 DEVELOPER 中包含了项目中一些核心类的定义，给开发者使用，可以通过它们编译动态连接库，在运行时调用。本文我们只看 SRC 中的架构，其目录如下

SRC
├── actor
├── analysis
│   ├── Makefile
│   ├── algorithm
│   ├── analysis
│   ├── analysis.tex
│   ├── dof_grp
│   ├── fe_ele
│   ├── handler
│   ├── integrator
│   ├── model
│   └── numberer
├── convergenceTest
├── coordTransformation
├── damage
├── database
├── domain
│   ├── component
│   ├── constraints
│   ├── domain
│   ├── groundMotion
│   ├── load
│   ├── loadBalancer
│   ├── node
│   ├── partitioner
│   ├── pattern
│   ├── region
│   ├── subdomain
│   └── ...
├── element
├── handler
├── interpreter
├── material
│   ├── Material.cpp
│   ├── Material.h
│   ├── nD
│   ├── section
│   ├── uniaxial
│   ├── yieldSurface
│   └── ...
├── modelbuilder
├── optimization
├── recorder
├── reliability
├── remote
├── system_of_eqn
├── tcl
└── ...

从文件夹中可以找到很多熟悉的名字。 domain 是用于存储整个模型的。 element 构建了各种各样的单元，这些单元依赖于 material 。section 在这里被看成了一种特殊的 material 。constraints 是模型的约束信息，node 是模型的节点信息，pattern 是模型中的荷载特征信息。coordTransformation 用于整体坐标与单元坐标的相互转换。 convergenceTest 用于判断是否收敛。integrator 用于将模型沿时间推移，建立非线性方程。algorithm 用于迭代求解非线性方程。 system_of_eqn 用于解线性方程，被 algorithm 所调用。 numberer 用于为自由度编号。 recorder 用于记录响应。

此外，还有用于特殊分析的 optimization 优化器，reliability 可靠度分析，damage 损伤分析。还有用于分布式计算的 subdomain actor 等。

下面我们来看架构。

UML 类图

首先来看 OpenSees 的 UML 类图。该图截于 Workshop 的 slide 中。

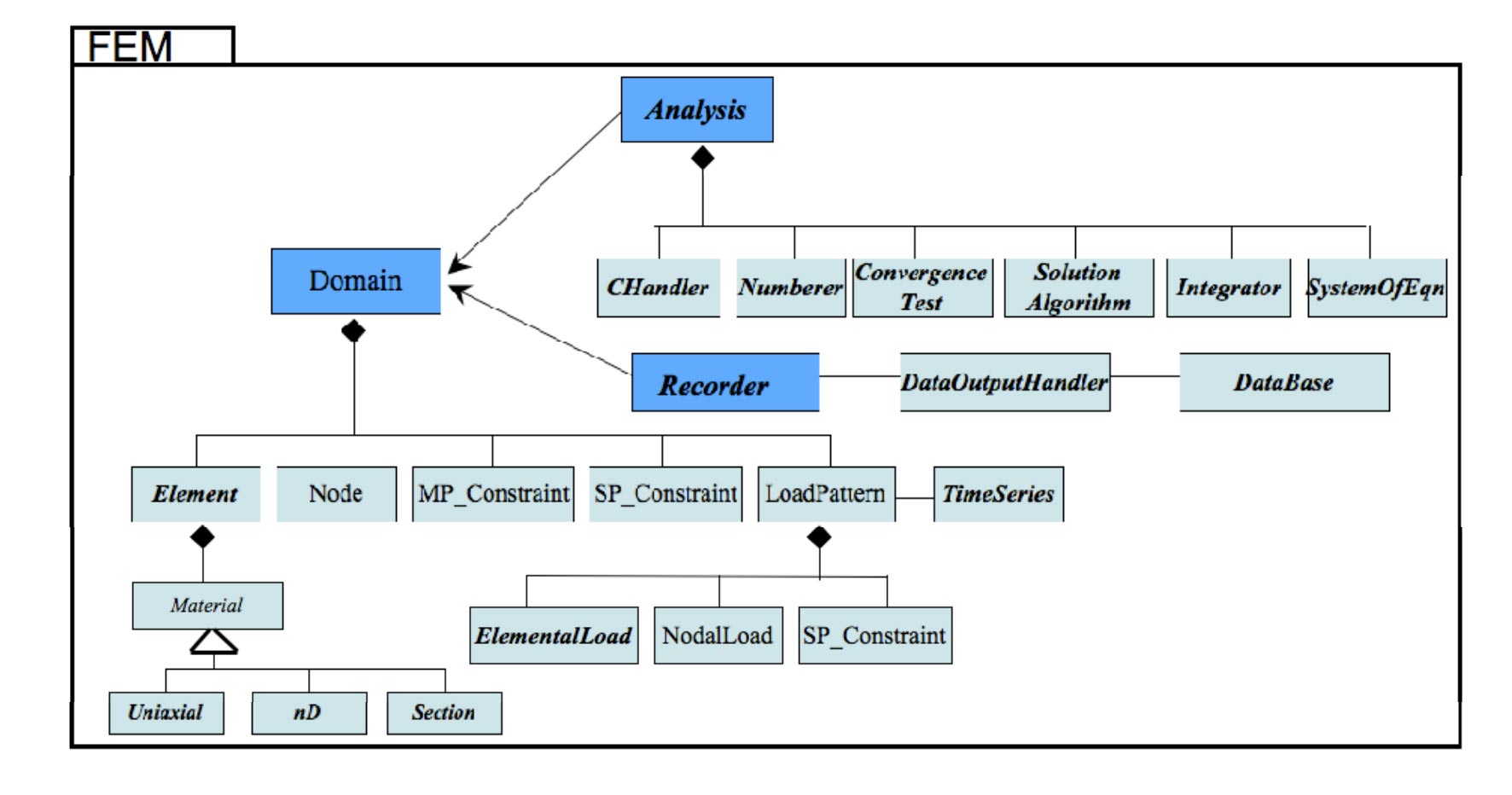
OpenSees是如何实现的

其中有三个主要的类。 Domain 记录的是物理模型的信息， Analysis 记录的是有限元模型的信息， Recorder 是结果记录器。可以看出，Domain 是最基本的类，另外两个类都是关联于它的。

Domain 中包含了几个对象的类，有 Element Node SP_Constraint MP_Constraint LoadPattern 。

这里 Element 是最核心的类， Element 中包含了 Material 类。OpenSees 的强大材料非线性分析能力得益于丰富的 Element 和 Material 库。Material 作为基类，派生出了单轴材料 Uniaxial，多轴材料 nD，以及截面 Section 。

Node 存储了节点信息，SP_Constraint 和 MP_Constraint 分别存储了单点约束和多点约束信息。

LoadPattern 存储了荷载信息。它包含了 ElementalLoad NodalLoad 和 SP_Constraint 。它还与一个类 TimeSeries 相关联，用于调整它加载到结构上的比例。

那么 OpenSees 执行分析 analyze 时是具体如何实现的呢？

OpenSees 执行分析的过程

创建模型

用户首先使用 model 命令创建一个 Domain 。model 命令中要输入一个 ModelBuilder ，通常情况下这里使用 BasicBuilder 或简写为 basic 。这个设置笔者认为是开发者原本想提供一些模板，类似于 SAP2000 新建模型时的模板供用户选择，但是没有实现。所以目前只支持这一种。ModelBuilder 也支持建立分布式的模型。

model 命令同时还要输入模型的几何空间 ndm 和自由度数 ndf 。

model 命令运行后，在 tcl 解释器中会注册其它操作 Domain 的命令，包括添加节点、单元等。用户可运行这些命令，把需要的模型添加到 Domain 中。

创建分析模型

模型添加好后，是指定 analysis 用的一些模块。

首先运行 constraints 命令。运行后建立一个派生于 ConstraintHandler类的实例。它实现一个 handle() 方法，用来施加节点的约束。

然后是 numberer 命令。运行后实例化一个派生于 DOF_Numberer 类的对象。它实现一个 numberDOF() 方法，用于对节点自由度进行编号。

在处理好自由度编号后，会在 Domain 的基础上生成一个分析用的模型 AnalysisModel ，保存了分析用的信息。

使用 Integrator 推移时间

下面介绍 integrator 命令。运行后建立一个派生于 Integrator 类的实例。它是用于推进结构分析的。Integrator 的主要任务是组建一个平衡方程 $\mathbf{A}\mathbf{x}=\mathbf{B}$。这个方程的意义是与 integrator 的类型有关的。对于静力情况，一般 $\mathbf{A}$ 表示结构的刚度矩阵，$\mathbf{B}$ 表示结构外力，$\mathbf{x}$ 则表示结构位移。而对于动力情况，不同的积分方式会导致这个矩阵的意义各有不同。例如，常用的隐式时间积分，Newmark-β 法中，递推公式为

$$\begin{aligned}\dot{\mathbf{u}}_{i+1}&=\dot{\mathbf{u}}_i+\Delta t\cdot\ddot{\mathbf{u}}_\gamma \\ &=\dot{\mathbf{u}}_i+\Delta t\cdot(1-\gamma)\ddot{\mathbf{u}}_i+\gamma\ddot{\mathbf{u}}_{i+1}\quad 0\leq\gamma\leq1\end{aligned}$$

$$\begin{aligned}\mathbf{u}_{i+1}&=\mathbf{u}_i+\Delta t\cdot\dot{\mathbf{u}}_i+\frac{1}{2}{\Delta t}^2\cdot\ddot{\mathbf{u}}_\beta\\&=\mathbf{u}_i+\Delta t\cdot\dot{\mathbf{u}}_i+\frac{1}{2}{\Delta t}^2\cdot(1-2\beta)\ddot{\mathbf{u}}_i+2\beta\ddot{\mathbf{u}}_{i+1}\quad 0\leq 2\beta\leq 1\end{aligned}$$

$$\mathbf{M}_{i+1}\ddot{\mathbf{u}}_{i+1}+\mathbf{C}_{i+1}\dot{\mathbf{u}}_{i+1}+\mathbf{K}_{i+1}\mathbf{u}_{i+1}=-\mathbf{M}_{i+1}\ddot{\mathbf{u}}_{g, i+1}$$

把 $i$ 时刻的状态看作已知量，可以看出，上面的迭代公式中有三个方程，三个未知量 $\ddot{\mathbf{u}}_{i+1}$ 、 $\dot{\mathbf{u}}_{i+1}$ 、 $\mathbf{u}_{i+1}$，可以求解。

因此，对于 Newmark 法，Integrator 也建立了一个方程 $\mathbf{A}\mathbf{x}=\mathbf{B}$ 。其中 A 和 B 可以从当前时刻的状态中得出，而其解就是下一个时刻的状态。

探索完 Integrator 的概念，我们再来看 Integrator 类做了什么事。首先，Integrator 的一个重要功能是：在任何时间点组装 A 和 B。调用的函数主要有 formEleTangent() formNodTangent() formEleResidual() formNodeUnbalance() 等。把 A 和 B 以特定的数据结构存储在 LinearSOE 中。这个功能会在迭代时被 Algorithm 调用，以获取任何时刻的结构状态。

在分析时，Integrator 主要做以下几件事

预测时间步长，并用 newStep() 方法在 AnalysisModel 中设置 trial 时间步。这时结构的荷载随时间发生改变。
调用 Algorithm.solve() 来求解 $\mathbf{A}\mathbf{x}=\mathbf{B}$，用得到的 x 来更新 AnalysisModel 。
如果求解成功，调用 commit() 提交新的状态。

可见，Integrator 类完成了非线性分析的最主要工作。当然，这些工作离不开 Algorithm 、 LinearSOE 和 ConvergenceTest 类的支持。以下我们分别来看它们做了什么。

Algorithm 类用于非线性方程组求解

在 Integrator 将结构的时间向后推移之后，结构的平衡被打破。这时，就需要用一个非线性求解器来求解结构新的平衡状态。这时就要用到 Algorithm 类。Algorithm 类有两种派生形式，分别是 EquiSolnAlgo 用于解非线性方程，另一种是 eigenAlgo 类，用于解特征值。

在 tcl 中运行 algorithm 命令后，就会实例化一个派生于 EquiSolnAlgo类的对象。它通过调用 solveCurrentStep() 函数来进行迭代求解。

以最常用的 Newton-Raphson 法为例，它定义于派生类 NewtonRaphson 中。它在每次迭代时，使用当前状态下，结构的切线刚度矩阵和结构的初始切线刚度矩阵的线性组合进行搜索。这样，就建立了一个搜索用的 A 矩阵。

A 矩阵和 B 向量都确定了后，就可以求解线性方程组了。这个求解是通过 LinearSOE 来完成的。得到了线性方程组的解后，更新 AnalysisModel 。会发现，由于非线性的存在，结构并不一定是平衡的。

结构是否平衡，是通过 ConvergenceTest 类来完成判断的。如果目前结构没有平衡，Algorithm 会进行迭代。迭代时依据现在的状态重新建立 A 和 B ，再次求解线性方程组，直到 ConvergenceTest 认为这一步完成了收敛。再将结果通知 Algorithm 。

LinearSOE 用于线性方程组求解

当用户运行 system 命令时，实例化一个派生于 LinearSOE 类的实例。这是一个线性方程组的存储器和求解器。

Algorithm 的 form...() 方法是用于建立 A 和 B 的，得到的 A 和 B 要存储在 LinearSOE 中。存储时是调用 LinearSOE 定义的 zero_A() zero_B() add_A() add_B() 等方法来完成的。

对于不同的 LinearSOE ，可以选择不同的存储方法。最容易理解的 FullGeneral 方法就是把 A 矩阵的每一个元素都存储起来。这也是 OpenSees 唯一支持的打印矩阵的存储方式。但是 A 矩阵通常是一个大型的对称稀疏矩阵，存储所有元素会占用大量不必要的内存。因此，可以选用不同的方式来减小内存用量。比如 BandGeneral ，就是把 A 调整为带状对称矩阵，并用列数为半带宽来的稠密矩阵来存储。

每个一 LinearSOE 都对应一个 Solver，用于求解。这个 Solver 可以用经典的 LAPACK fortran 程序来实现，也可以用流行的支持 CUDA 的 GPU 来实现。

求解的结果，通过 get_X() 等方法，由 Integrator 获取，再施加在结构中。

ConvergenceTest 用于判断收敛

由于结构存在非线性，需要迭代求解。迭代器采用浮点运算，无法完全使 $\mathbf{A}\mathbf{x}=\mathbf{B}$ 成立，而是有一个很接近于 $\mathbf{0}$ 的误差。ConvergenceTest 就定义了如何判断这个误差小到可以认为是方程是成立的。

用户运行 test 命令时，就会实例化一个 ConvergenceTest 派生类的实例。它有两个主要方法。 start() 用于初始化，而 test() 用于计算误差函数的值。每一步计算得到的误差 norm 都会保存起来。

每一种 ConvergenceTest 都会定义一个误差函数，这一函数是基于 A B 和 X 的。例如，CTestNormUnbalance 的误差函数为

$$\mathrm{norm}=||B||_n$$

即不平衡力的n范数。

再如，CTestEnergyIncr 的误差函数为

$$\mathrm{norm} = \sqrt{\Delta X\cdot B}$$

即位移的增量与力的内积，在多数情况下，代表结构是能量的增量。

材料非线性的实现

前文讨论过，OpenSees 的材料非线性主要是通过 Element 和 Material 来实现的。实现的方法是通过保存状态。

在OpenSees中，Domain Node Element Material 等类都是有状态的。状态的意思，是在时间推移的过程中，在每个时间点所记录下来的所需要存储的信息。

状态分为两种，分别是 trial 状态和 committed 状态。trial 表示在 Integrator 的带领下，结构正在试图将时间向后推移时，所保存的状态。而 committed 状态则是记录了在这次搜索之前，结构处于平衡态时，所保存的状态。

在分析中，Integretor 调用 newStep() 时，把 committed 状态复制一份，成为 trial 状态，然后把它认为需要推移的时间作用在 AnalysisModel 中。这时，trial 状态被改写，此时结构处于不平衡的状态。然后 Integrator 调用 solve()，通过非线性求解器 Algorithm 的迭代和线性求解器 LinearSOE 的求解，把结构 trail 的不平衡状态更新为新的平衡状态。此时如果 convergenceTest 判断新的 trial 状态达到了平衡，则 integrator 把 trial 状态复制成为新的 committed 状态，则完成了时间的一步推进。

这里要注意的是，time 的概念是与 timeSeries 的定义有关的。并不是完全等同于时间，而是通常所说的“伪时间”。因此，时间推移并不一定是 time 增大，而是指分析一步一步地向下进行。在静力分析中，time 指的是 pattern 中定义的力的比例。因此在 OpenSees 代码中，有时会使用 time 表示，而有时使用 lambda 来表示。

有了状态，就可以记录历史。例如，对于一个 Material ，可以在 committed 中记录它当前的应变方向，那么在 trial 时，就可以判断应变是否发生了反向。再如，可以在 committed 中记录当前的最大应变，就可以在 trial 时，判断材料发生了多大的损伤。

Material 实现的函数主要是 setTrialStrain(strain, strainRate) 。即给定 trial 的应变和应变率，更新材料的 trial 状态。并可以在 Element 需要时，提供刚度和应力等信息。

用这种方式，在 Algorithm 迭代时，每进行一次迭代，都会把得到的 X 更新到 AnalysisModel 中。再依此计算材料相应的 strain 和 strainRate，再更新材料状态。再把更新后的状态组成新的 A 和 B ，进行下一步的迭代。

几何非线性的实现

OpenSees 的几何非线性是通过 CrdTransf 类来实现的。它定义为 Element 的成员。

用户调用 geomTransf 时，就会实例化一个派生于 CrdTransf 类的实例。如果输入 Linear，则为 LinearCrdTransf，进行小变形变换。如果输入 Corotational ，则为 CorotCrdTransf ，进行大变形变换。

顾名思义，CrdTransf 是用于进行坐标变换的。它把在全局坐标和单元局部坐标之间相互变换。

LinearCrdTransf 在获取节点坐标时，使用的是初始状态下的坐标。而 CorotCrdTransf 在获取节点坐标时，是上一步变形后节点所处状态的坐标，以此实现了大变形的处理。

这里的坐标除了 global 和 local 两个体系外，还有一个 basic 的概念。 basic 坐标系统是去除了不会产生单元内力的刚体位移后的坐标体系。例如小变形二维欧拉梁单元，其 local 坐标有六个自由度，单元刚度矩阵为

$$\mathbf{A}_{\mathrm{local}} = \begin{bmatrix}\frac{EA}{l} & 0 & 0 & -\frac{EA}{l} & 0 & 0 \\0 & \frac{12EI}{l^3} & \frac{6EI}{l^2} & 0 & \frac{-12EI}{l^3} & \frac{6EI}{l^2} \\0 & \frac{6EI}{l^2} & \frac{4EI}{l} & 0 & \frac{-6EI}{l^2} & \frac{2EI}{l} \\\frac{-EA}{l} & 0 & 0 & \frac{EA}{l} & 0 & 0 \\0 & \frac{-12EI}{l^3} & \frac{-6EI}{l^2} & 0 & \frac{12EI}{l^3} & \frac{-6EI}{l^2} \\0 & \frac{6EI}{l^2} & \frac{2EI}{l} & 0 & \frac{-6EI}{l^2} & \frac{4EI}{l}\end{bmatrix}$$

可以看到，有很多重复项。事实上，这时的 local 坐标系中的自由度并不是相互独立的，而是存在一定关联。在这个单元中，只有三个相互独立的自由度，在 OpenSees 中被称为 basic 系统。如果把 basic 体系下的力标为 q ，位移标为 v，则 q 有三个分量，分别代表单元的轴力和两端弯矩，对应为 v 为轴向变形和两端转角。如果把 global 体系下的力标记为 p ，位移标为 u，则 basic 体系和 global 体系的关系如下

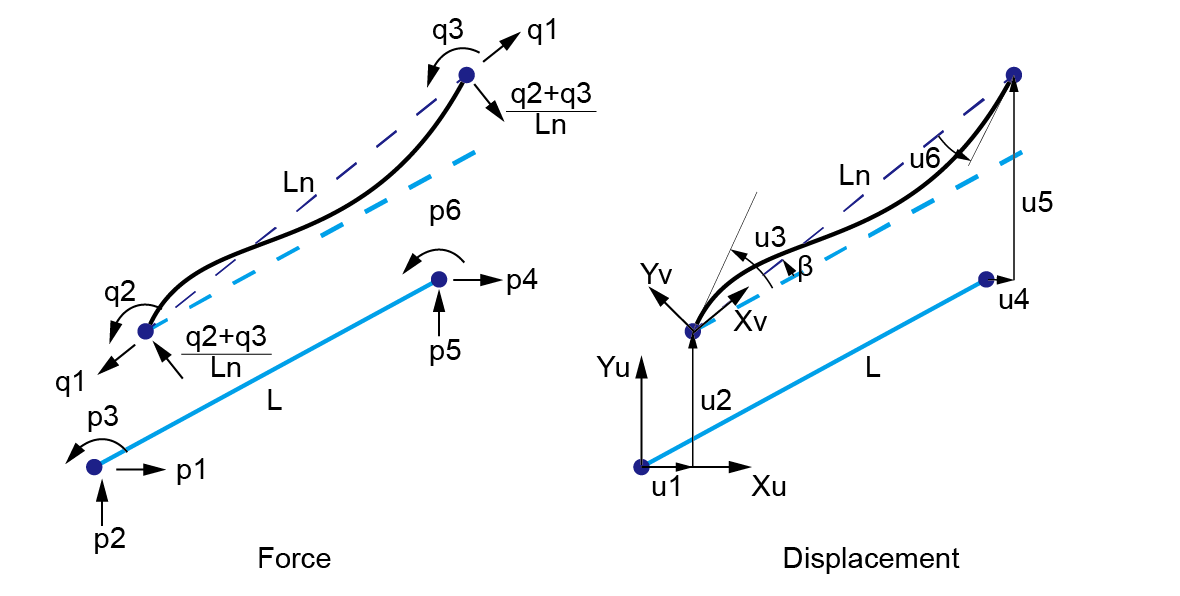
OpenSees的basic体系是什么

basic 体系下的位移可以这样计算

$$\begin{aligned}v_1 = L_n - L \\v_2 = u_3 - \beta \\v_3 = u_6 - \beta \\\end{aligned}$$

写成变换矩阵的形式，即为

$$\mathbf{a}_g(\mathbf{u}) = \frac{\partial \mathbf{v}}{\partial \mathbf{u}}$$

位移的变换矩阵可以同样作用于力的变换

$$\mathbf{q} = \mathbf{a}_g^T(\mathbf{u}) \mathbf{p}$$

其中，变换矩阵 $\mathbf{a}_g(\mathbf{u})$ 就是通过 CrdTransf 类来保存的。在 LinearCrdTransf 中，它是一个常矩阵。而在 CorotCrdTrasf 中才是与位移 u 有关的矩阵。除此之外， CrdTransf 还保存了单元的长度信息。

这样，在 basic 体系下，小变形欧拉梁的刚度矩阵可以写成如下形式

$$A_{\mathrm{basic}} = \begin{bmatrix}\frac{EA}{l} & 0 & 0 \\0 & \frac{4EI}{l} & \frac{-2EI}{l} \\0 & \frac{-2EI}{l} & \frac{4EI}{l}\end{bmatrix}$$

而如果是大变形，则需要通过其它信息计算。

OpenSees 是如何实现的

文件树