OpenSees 分析参数的选择方法（上）-翰林苑|董翰林的个人网站

在结构力学中，我们知道，结构的线性分析一般流程如下：

为结构中的节点和单元编号，并建立整体坐标系；
对各单元计算局部坐标系下的单元刚度矩阵 $\bm{\bar{K}^e}$ ，并通过坐标变换矩阵 $\bm{T}$ ，形成整体坐标系下的单元刚度矩阵 $\bm{K^e}$ ；
根据结构的约束，对自由度编号，并将单元刚度矩阵拼装为整体刚度矩阵 $\bm{K}$ ；
由节点荷载和单元荷载计算荷载向量 $\bm{F}$ ；
建立线性方程组 $\bm{K\Delta}=\bm{F}$ ，并解出 $\bm{\Delta}$ ;
将 $\bm{\Delta}$ 分解为各单元位移 $\bm{\Delta^e}$ ，再与单元刚度矩阵相乘，得到单元受力 $\bm{F^e}=\bm{K^e\Delta^e}$

但是对于非线性分析，操作就比较复杂了。这是因为，刚度矩阵是随结构的受荷状态不断变化的，因此无法通过求解一个线性方程组完成分析。非线性分析的基本思路是，把整个分析过程转化为一系列分析步，然后在每一分析步中进行迭代，每一次迭代是求解一个非线性方程组。这样，通过两层迭代，才能完成非线性分析。

在迭代的过程中，涉及到很多步骤。对于很多商业软件，这些步骤都是由计算机自动选取的。但是对于 OpenSees 来说，由于科研工作者需要软件的操作基本可控，因此它没有自动选择这些参数，而是需要用户来指定。但是对于初学者来说，选取合适的参数比较困难。所以，本文就是为初学者了解 OpenSees 分析时使用的参数都是做什么而准备的。

算法流程

首先来回顾一下 OpenSees 进行非线性分析的算法流程。不论是静力分析还是动力分析，在执行 analyze 命令的时候，是这样循环的：

for (int i = 0; i < numIncr; i++) {
    theIntegrator -> newStep();
    theAlgorithm -> solveCurrentStep();
    theModel -> commit();
}

for 语句中的 i ，就是用户定义在 analyze 命令中的参数，就是把整个分析的过程由用户定义成小的分析步的步数。在每一步中，首先使用 integrator 的 step() 方法，改变当前模型的状态。例如对于 LoadControl ，就是在模型中增加一些力。此时模型的平衡被打破。然后，再使用 algorithm 中的 solveCurrentStep() 方法，将模型中被打破的平衡通过迭代，使之重新恢复平衡。每一次迭代后模型的状态是暂时保存的，称为 trial 状态。迭代的收敛是通过 test 来判断的。如是 test 判断出结构成功地再次平衡了，则进入第三步，调用 commit() 方法，将结构中的 trial 状态更新为 committed 状态。这样，这一分析步就完成了。

上面提到了 OpenSees 控制参数中的 integrator, algorithm, test，除此之外，还有用于处理约束条件的 constraint，用于处理自由度编号的 numberer 和用于处理矩阵存储方式的 system，以及区分静力分析和动力分析的 analysis 。下面对它们的用法一一介绍。

Constraint

constraint 命令用于指定如何处理模型中的约束。模型中的约束分为两种，分别是单点（Single Point）约束 SP_Constratint 和多点（Multiple Point）约束 MP_Constraint 。其中：

单点约束，是指对结点本身的约束，如 fix 代表节点的自由度约束，即支座。此外还有外加位移等。

多点约束，是指多个结点之前的关系的约束，比如两个自由度相等 equalDOF ，平面约束 diaphragm 和刚体约束 rigidBody 等。

Transformation

Transformation 是通过节点的约束确定一个转移矩阵 $\bm{T}$ ，将这一矩阵与总体刚度矩阵相乘，即可得到去掉了约束自由度的非奇异总刚矩阵，即：

$$ \bm{K}^* = \bm{T}^T\bm{K}\bm{T} $$

对于受力也使用同样的方式处理，即：

$$ \bm{F}^* = \bm{T}^T\bm{F} $$

这样，可以建立线性方程组：

$$ \bm{K}^* \bm{\Delta}_r = \bm{F}^* $$

下面用一个简单的例子说明。对于一个图示的悬臂梁

悬臂梁的刚度矩阵

其总刚度矩阵与单元刚度矩阵相同，为：

$$\bm{K} = \begin{bmatrix}\frac{EA}{l} & 0 & 0 & -\frac{EA}{l} & 0 & 0 \\0 & \frac{12EI}{l^3} & \frac{6EI}{l^2} & 0 & \frac{-12EI}{l^3} & \frac{6EI}{l^2} \\0 & \frac{6EI}{l^2} & \frac{4EI}{l} & 0 & \frac{-6EI}{l^2} & \frac{2EI}{l} \\\frac{-EA}{l} & 0 & 0 & \frac{EA}{l} & 0 & 0 \\0 & \frac{-12EI}{l^3} & \frac{-6EI}{l^2} & 0 & \frac{12EI}{l^3} & \frac{-6EI}{l^2} \\0 & \frac{6EI}{l^2} & \frac{2EI}{l} & 0 & \frac{-6EI}{l^2} & \frac{4EI}{l}\end{bmatrix}$$

在处理左端的固定支座时，使用的转移矩阵为

$$\bm{T} = \begin{bmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} $$

即从单位矩阵中把约束过的自由度的行去掉。这样，可以得到：

$$\bm{K}^* = \bm{T}^T\bm{K}\bm{T} = \begin{bmatrix} \frac{EA}{l} & 0 & 0 \\ 0 & \frac{12EI}{l^3} & \frac{-6EI}{l^2} \\ 0 & \frac{-6EI}{l^2} & \frac{4EI}{l}\end{bmatrix} $$

对于外力，假设受一个单位侧向集中力，未经处理的外力向量为：

$$\bm{F} = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix}^T $$

处理后为：

$$\bm{F}^* = \bm{T}^T\bm{F} = \begin{bmatrix} 0 & 1 & 0 \end{bmatrix}^T $$

目前， OpenSees 不支持一个节点同时存在单点约束和多点约束，如果出现一个点同时有这两种约束时，会出现提示：

1	TransformationConstraintHandler::handle() - error in logic

在大多数情况下，都是模型的问题。这时需要检查模型。比如，一个点被完全约束，而另一个点与这个点又加了多点约束。正确的做法是，将另一个点直接使用单点约束。

如果不得不同时使用单点约束和多点约束，可以尝试下面的 Penalty 法或 Lagrange 法。

Plain

Plain 方法是我们最常使用到的方法，即划行划列法。即把设置了支座的自由度对应的行和列划掉，再把多点约束的自由度合并。得到的结果与 Transformation 是一样的。

Plain 法与 Transformation 法一样，不支持一个节点同时存在单点约束和多点约束。如果出现，会有提示

1	WARNING PlainHandler::handle() - constraint at dof 1 already specified for constrained node in MP_Constraint at node 1

遇到这个提示时，则需要检查模型的约束了。

Lagrange

使用 Lagrange 法施加约束，不但不会减少自由度，还会增加矩阵的维度。表达式为：

$$ \begin{bmatrix}\bm{K} & \bm{C}^T \\ \bm{C} & \bm{0}\end{bmatrix} \begin{bmatrix}\bm{\Delta} \\ \bm{\lambda}\end{bmatrix} = \begin{bmatrix}\bm{F} \\ \bm{Q}\end{bmatrix}$$

这里的 $\bm{C}$ 与 Transformation 中的 $\bm{T}$ 的取法刚好相反，是把有约束的自由度取为 1（或用户指定的值），无约束的自由度取为 0 。这里为：

$$ \bm{C} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0\end{bmatrix} $$

这里矩阵维度增加了很多。因此，只有在 Transformation 无法处理的单点有多约束的情况下，才可选用这一方法。否则应使用 Transformation 方法。

Penalty

Penalty 法即罚函数法，通过将刚度矩阵中，有约束的位置的刚度加上一个较大的罚数，使总刚度矩阵满秩，这样就可以不用划去行列，得到线性方程组的解。但是约束部分的位移不是绝对约束的，而是有一个较小的位移。罚函数法可以理解为给了支座一个很小的初始位移后的结构。

$$ \left[\bm{K}+\bm{C}^T\bm{\alpha}\bm{C}\right]\bm{U} = \left[\bm{R}+\bm{C}^T\bm{\alpha}\bm{Q}\right] $$

Numberer

numberer 命令用于对自由度进行编号。在分析模型中，自由度的编号与 tag 的顺序无关，而是通过一定的编号规则来排序的。对于不同规模的模型，宜使用的编号规则也不相同。 OpenSees 中，可以使用的有 Plain RCM 和 AMD 三种。

Plain

Plain 是指不需要特别的排序方式。结构中的结点是如何保存的，则按什么顺序来排序。这种排序方式适用于两种情况：

结构的规模很小，结点不多，排序方式不同不会引起内存占用的大幅变化。
使用稀疏矩阵求解器来进行分析，因为求解器本身会对矩阵中的元素进行排序，所以无需在这里进行排序。

对于正常使用的规模不大的大多数问题，都可以直接使用 Plain 排序方式来实现。

RCM

RCM 是指 Reverse Cuthill-McKee 排序法。由于结构的刚度矩阵通常为稀疏的正定对称矩阵，对其自由度适当排序后，可以减小刚度矩阵的带宽。这样，如果使用带宽法来存储矩阵，可以大幅减小占用的空间。这里引用多伦多大学 Oh-sung Kwon 教授的两张图片来表达使用 RCM 方法后矩阵占用内存的变化。

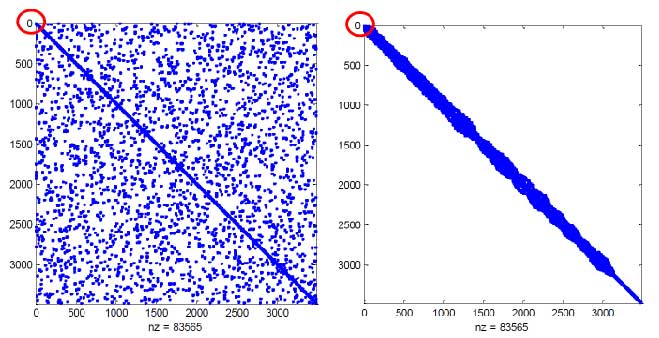
OpenSees自由度排序

图中每一个点表示一个稀疏矩阵中的非零元素。左图表示没有排序时，非零元素是分散的，用带宽法存储时占用空间较大，为 92.4 MB 。而右图是排序后，非零元素全部分布在对角线附近，可以很紧凑地使用带宽法来保存矩阵，仅占用了0.97 MB 。

但是对于自由度较少的情况，使用这一排序规则不一定可以节约空间，甚至还会增加使用的空间。因此，对于大型结构，宜使用这种方法。而对于小型结构，使用 Plain 就足够了。

AMD

AMD 表示 Alternative_Minimum_Degree 排序法，和 RCM 法实现的效果是相同的，只是使用了另外一种排序方法。该法是 1996 年提出， 2004 年完善的。而 RCM 法是 1969 年提出的。

System

system 命令其实是 system of equations 的简写，代表结构中的线性方程组的存储和求解方式。 OpenSees 中提供了很多种方式，我们来一一介绍。

BandGeneral

BandGeneral 是一种用于带状矩阵的存储方法。对于一个 $n\times n$ 带状矩阵，其形状可以用两个常数 k1 和 k2 确定，分别表示左侧和右侧的半带宽。则矩阵的总带宽为 k1+k2+1 。例如，对于一个带宽为 3 的 6x6 矩阵：

$$\begin{bmatrix} B_{11} & B_{12} & 0 & \cdots & \cdots & 0 \\ B_{21} & B_{22} & B_{23} & \ddots & \ddots & \vdots \\ 0 & B_{32} & B_{33} & B_{34} & \ddots & \vdots \\ \vdots & \ddots & B_{43} & B_{44} & B_{45} & 0 \\ \vdots & \ddots & \ddots & B_{54} & B_{55} & B_{56} \\ 0 & \cdots & \cdots & 0 & B_{65} & B_{66} \end{bmatrix}$$

可以用以下的 6x3 矩阵来表示

$$\begin{bmatrix}0 & B_{11} & B_{12} \\ B_{21} & B_{22} & B_{23} \\ B_{32} & B_{33} & B_{34} \\ B_{43} & B_{44} & B_{45} \\ B_{54} & B_{55} & B_{56} \\ B_{65} & B_{66} & 0 \end{bmatrix}$$

对于这样表示的矩阵，在 Lapack （使用 Fortran 编写的线性代数快速求解器）中提供了 DGBSV 和 SGBTRS 两个方法来求解。

BandGeneral 是一个一般问题中较常用的储存方式。

BandSPD

BandSPD 中，Band 表示带状矩阵， SPD 表示对称正定矩阵（Symmetric Positive Definite）。由于其对称性，可以只储存带宽的一半。如 6x6 矩阵

$$\begin{bmatrix}A_{11} & A_{12} & A_{13} & 0 & \cdots & 0 \\ & A_{22} & A_{23} & A_{24} & \ddots & \vdots \\ & & A_{33} & A_{34} & A_{35} & 0 \\ & & & A_{44} & A_{45} & A_{46} \\ & sym & & & A_{55} & A_{56} \\ & & & & & A_{66}\end{bmatrix}$$

则可以使用以下矩阵储存

$$\begin{bmatrix}A_{11} & A_{12} & A_{13} \\ A_{22} & A_{23} & A_{24} \\ A_{33} & A_{34} & A_{35} \\ A_{44} & A_{45} & A_{46} \\ A_{55} & A_{56} & 0 \\ A_{66} & 0 & 0\end{bmatrix}$$

在 Lapack 中，也提供了对于这样的结构的求解器 DPBSV 和 DPBTRS 。

对于弹性结构，刚度矩阵一定是对称正定的，可以使用这种保存方式。对于非线性结构，有时刚度矩阵不一定对称正定。

ProfileSPD

对于对称正定稀疏矩阵，还有一个更紧凑的存储方法，就是 ProfileSPD 。这里把矩阵扁平化为一个向量，并去掉所有首尾开始的连续的零元素。但是需要另外存储一个位置向量，记录对角元素的位置。比如，有如下对称正定稀疏矩阵：

$$ \begin{bmatrix}A_{11} & A_{12} & 0 & 0 & 0 \\ & A_{22} & A_{23} & 0 & A_{25} \\ & & A_{33} & 0 & 0 \\ & & & A_{44} & A_{45} \\ & sym & & & A_{55} \end{bmatrix} $$

可以使用以下两个一维向量存储：

$$ \begin{bmatrix} A_{11} & A_{12} & A_{22} & A_{23} & A_{33} & A_{44} & A_{25} & 0 & A_{45} & A_{55} \end{bmatrix} $$

$$ \begin{bmatrix} 1 & 3 & 5 & 6 & 10 \end{bmatrix} $$

该方法进一步地优化了内存使用。

FullGeneral

FullGeneral 没有采用任何内存优化措施，因此对于大型结构会消耗大量内存。但是使用 FullGeneral 有一个好处是，可以使用 printA 命令查看结构的总体刚度矩阵。使用其它选项时，是不支持这一点的。

SuperLU

SuperLU 是一个开源的稀疏矩阵线性方程组求解器。使用 C 语言编写，可供 Fortran 和 C 用。支持并行和分布式计算，支持 MPI, OpenMP 和 CUDA 。详细信息见这里。

UmfPack

UmfPack 是另一个用 C 写成的大型稀疏矩阵线性方程组求解，也支持 CUDA 等 GPU 并行计算。详细信息见这里。

Cusp

Cusp 是另一个使用了 GPU 的求解器。没有包含在 OpenSees 中，如果需要使用，需要额外的配置。

以上可以使用 CUDA 进行 GPU 并行计算的选项对于有支持 CUDA GPU 的用户来说，可能得到更快的结果。

Test

test 命令的全称是 Convergence test 。它的作用是判断一个分析步是否收敛。判断的依据就是结构总体的线性方程组 $\bm{F} = \bm{K}\bm{\Delta}$ 是否满足其收敛条件。不同的参数对应不同的收敛条件。

判断方式可以分为两类，一类是通过增量判断，一类是通过增量的相对值判断。这里的增量是指这一分析步的增量，也就是线性方程组中的值，而不是每一个迭代步相对于上一步的增量。而相对值，是指迭代后的值与迭代开始时值的比值。下面我们一一来看。

EnergyIncr

EnergyIncr 的全称是 Energy Increment ，即能量增量。能量即力与位移的乘积。这里的计算方法为：

$$ \frac{1}{2}\bm{\Delta}^{(i)}\cdot\bm{F}^{(i)} < \varepsilon $$

式中，(i) 表示第 i 个迭代步，$\varepsilon$ 表示用户指定的临界值 tol 。

这里注意 OpenSees Wiki 里面的公式有误，没有在前面乘以 1/2 。在源代码中是乘以了 1/2 的。这里的能量指的是弹性应变能。

值得注意的是，能量的单位在这里为位移与力的乘积。在考虑临界值 $\varepsilon$ 的取值时，需要注意单位。

对于临界值的取值，要根据模型实际使用的单位和受力、位移的水平来确定。在我认为，比结构的受力水平小三个数量级，一般就可以接收。比如，对于受力（集中力）为 1 ~ 10 数量级，位移也为 1 ~ 10 数量级的结构，可取能量的临界值为 1e-3 x 1e-3 = 1e-6。而如果是力或位移的临界值，则可取 1e-3 。过小的临界值可能会造成非线性结构的收敛困难。而且得到的高精度小数的工程意义不大。但是如果精度不足，可能会导致误差累积，在非线性求解过程中结果如现较大偏差。因此，可以在分析时，使用不同数量级的临界值分别计算，然后根据误差选择一个较为合理的值。

RelativeEnergyIncr

RelativeEnergyIncr 指的是能量增量的相对值。计算方法为：

$$ \frac{\bm{\Delta}^{(i)}\cdot\bm{F}^{(i)}}{\bm{\Delta}^{(0)}\cdot\bm{F}^{(0)}} < \varepsilon $$

NormUnbalance

NormUnbalance 即力增量的范数。这里默认使用的是二范数，即向量的模。计算方法为：

$$ \parallel \bm{F}^{(i)} \parallel = \sqrt{\bm{F}^{(i)^T}\bm{F}^{(i)}} < \varepsilon $$

用户也可以指定使用其它范数。但物理意义不明显。

RelativeNormUnbalance

$$ \frac{\parallel \bm{F}^{(i)} \parallel}{\parallel \bm{F}^{(0)} \parallel} < \varepsilon $$

NormDispIncr

$$ \parallel \bm{\Delta}^{(i)} \parallel < \varepsilon $$

RelativeNormDispIncr

$$ \frac{\parallel \bm{\Delta}^{(i)} \parallel}{\parallel \bm{\Delta}^{(0)} \parallel} < \varepsilon $$

RelativeTotalNormDispIncr

这个名字有点长。与以上仅检验最后一个迭代步不同，它检验的是这一分析步的位移范数与所有分析步中位移范数之和的比。计算方法为：

$$ \frac{\parallel \bm{\Delta}^{(i)} \parallel}{\sum_{n=0}^{i}\parallel \bm{\Delta}^{(n)} \parallel} < \varepsilon $$

FixedNumIter

FixedNumIter 是指不论是否收敛，只分析一定的步数。它只能用于混合模拟中，必须与混合模拟特定的 integrator 配合使用。

其它分析命令 algorithm integrator analysis eigen analyze 将在后续文章中介绍。敬请关注。

OpenSees 分析参数的选择方法（上）

算法流程

Constraint

Transformation

Plain

Lagrange

Penalty

Numberer

Plain

RCM

AMD

System

BandGeneral

BandSPD

ProfileSPD

FullGeneral

SuperLU

UmfPack

Cusp

Test

EnergyIncr

RelativeEnergyIncr

NormUnbalance

RelativeNormUnbalance

NormDispIncr

RelativeNormDispIncr

RelativeTotalNormDispIncr

FixedNumIter

VISITORS

NAVIGATION