OpenSees 有两个解释器, TCL 和 Python 。由于 OpenSees 是由 C++ 编写的,所以也可以使用 C++ 直接调用 OpenSees 的核心。本文我们使用几种不同的方法来比较不同的调用方式的性能差异。
首先,介绍一下用于比较性能差异的问题。这里我们采用最常见的 OpenSees 例子,桁架的静力分析。如图所示。
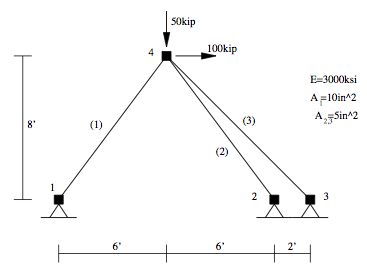
这一问题中采用的是英制单位,不过不必担心,我们这里不讨论这些数值有多大,只是探索其性能,所以仍保留使用英制单位。
为了放大性能的差异,我们把这一个问题拓展为一个参数化的问题。这里我们把水平力从 1 变化到 1,000,再把 A1 的面积从 1 变化到 10,取变化步长为 1 ,则构建了 10,000 个不同的模型。然后我们把这 10,000 个不同模型的顶点 4 的位移进行输出,直接在控制台打印。
下面通过不同的方式来用 OpenSees 解这一问题。
使用 TCL 脚本
这一问题的原 TCL 脚本可以在 这里 找到。下面我们来改动它,形成一个参数分析的脚本,并记录分析用时。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| proc parametric {fh a1} {
wipe
wipeAnalysis
model BasicBuilder -ndm 2 -ndf 2
node 1 0.0 0.0
node 2 144.0 0.0
node 3 168.0 0.0
node 4 72.0 96.0
uniaxialMaterial Elastic 1 3000
element truss 1 1 4 [expr $a1 * 1.0] 1
element truss 2 2 4 5.0 1
element truss 3 3 4 5.0 1
fix 1 1 1
fix 2 1 1
fix 3 1 1
pattern Plain 1 "Linear" {
load 4 [expr $fh * 1.0] -50
}
system BandSPD
constraints Plain
integrator LoadControl 1.0
algorithm Linear
numberer RCM
analysis Static
analyze 1
puts [nodeDisp 4]
}
set startTime [clock milliseconds]
for {set fh 1} {$fh <= 1000} {incr fh} {
for {set a1 1} {$a1 <= 10} {incr a1} {
parametric $fh $a1
}
}
set endTime [clock milliseconds]
puts "Time: [expr ($endTime - $startTime) / 1000.] s.
|
这个 TCL 脚本在原来脚本的基础上,把一次分析用一个 proc 包装,然后通过两个变量来循环,调用这个 proc ,完成参数化分析。
使用 Python 脚本
下面介绍使用 Python 脚本完成分析的代码。它的原脚本可以在 这里 找到。这里我们把它进行修改。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| import time
from openseespy.opensees import *
def parametric(fh: int, a1: int) -> None:
wipe()
model("BasicBuilder", "-ndm",2, "-ndf",2)
defaultUnits("-force", "kip", "-length", "in", "-time", "sec", "-temp", "F")
node(1, 0.0, 0.0)
node(2, 144.0, 0.0)
node(3, 168.0, 0.0)
node(4, 72.0, 96.0)
fix(1, 1, 1)
fix(2, 1, 1)
fix(3, 1, 1)
uniaxialMaterial("Elastic", 1, 3000.0)
element("truss", 1, 1, 4, a1 * 1.0, 1)
element("truss", 2, 2, 4, 5.0, 1)
element("truss", 3, 3, 4, 5.0, 1)
timeSeries("Linear", 1)
pattern("Plain", 1, 1, "-fact", 1.0)
load(4, fh * 1.0, -50.0)
system("BandSPD")
numberer("RCM")
constraints("Plain")
algorithm("Linear")
integrator("LoadControl", 1.0)
analysis("Static")
analyze(1)
print(nodeDisp(4))
if __name__ == "__main__":
startTime = time.time()
for fh in range(1, 1001):
for a1 in range(1, 11):
parametric(fh, a1)
endTime = time.time()
print("Time: ", endTime - startTime, "s")
|
Python 脚本也很简单,这里就不详细解释了。
使用 C++ 调用
下面我们详细介绍使用 C++ 直接调用的方法。为了方便,使用 Linux 系统。MacOS 没有测试,但是应该可以得到相同的效果。对于 Windows 用户,可以选择安装 WSL2 ,也可以下载安装 GNUWin32 编译器。这里就不过多介绍了。
如果你使用 docker ,可以拉取 hanlindong/opensees:developer 镜像,并在镜像中操作。
在源代码中,也可以找到使用 C++ 直接调用的代码。 GitHub 地址在 这里。同样地,我们在它的基础上进行修改。
首先,下载 OpenSees 的源代码。登录到 GitHub 的 OpenSees 仓库,看到左侧写有 master 的下拉菜单,展开,选择 tags 选项卡中的 v3.2.0 。由于 OpenSees 不断地在提交,最新分支上的代码不可避免地有冲突。所以回退到上一个发布的 tag 再下载。
点击右侧的绿色 Code 按钮,下载源代码。下载下来一个压缩文件,解压到 /home/ops/OpenSees 路径中。
在 EXAMPLES 文件夹中可以找到这个名为 Example1 的文件夹,打开,有一个 main.cpp 文件,是 C++ 代码。另一个是 Makefile 是用来编译 C++ 文件用的。
现在我们在 EXAMPLES 中再建立一个文件夹,命名为 Parametric 。在里面建立一个 C++ 文件,内容如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
| #include <stdlib.h>
#include <OPS_Globals.h>
#include <StandardStream.h>
#include <ArrayOfTaggedObjects.h>
#include <Domain.h>
#include <Node.h>
#include <Truss.h>
#include <ElasticMaterial.h>
#include <SP_Constraint.h>
#include <LoadPattern.h>
#include <LinearSeries.h>
#include <NodalLoad.h>
#include <StaticAnalysis.h>
#include <AnalysisModel.h>
#include <Linear.h>
#include <PenaltyConstraintHandler.h>
#include <DOF_Numberer.h>
#include <RCM.h>
#include <LoadControl.h>
#include <BandSPDLinSOE.h>
#include <BandSPDLinLapackSolver.h>
StandardStream sserr;
OPS_Stream *opserrPtr = &sserr;
int parametric(int fh, int a1)
{
Domain *theDomain = new Domain();
Node *node1 = new Node(1, 2, 0.0, 0.0);
Node *node2 = new Node(2, 2, 144.0, 0.0);
Node *node3 = new Node(3, 2, 168.0, 0.0);
Node *node4 = new Node(4, 2, 72.0, 96.0);
theDomain->addNode(node1);
theDomain->addNode(node2);
theDomain->addNode(node3);
theDomain->addNode(node4);
UniaxialMaterial *theMaterial = new ElasticMaterial(1, 3000);
Truss *truss1 = new Truss(1, 2, 1, 4, *theMaterial, a1 * 1.0);
Truss *truss2 = new Truss(2, 2, 2, 4, *theMaterial, 5.0);
Truss *truss3 = new Truss(3, 2, 3, 4, *theMaterial, 5.0);
theDomain->addElement(truss1);
theDomain->addElement(truss2);
theDomain->addElement(truss3);
SP_Constraint *sp1 = new SP_Constraint(1, 0, 0.0, true);
SP_Constraint *sp2 = new SP_Constraint(1, 1, 0.0, true);
SP_Constraint *sp3 = new SP_Constraint(2, 0, 0.0, true);
SP_Constraint *sp4 = new SP_Constraint(2, 1, 0.0, true);
SP_Constraint *sp5 = new SP_Constraint(3, 0, 0.0, true);
SP_Constraint *sp6 = new SP_Constraint(3, 1, 0.0, true);
theDomain->addSP_Constraint(sp1);
theDomain->addSP_Constraint(sp2);
theDomain->addSP_Constraint(sp3);
theDomain->addSP_Constraint(sp4);
theDomain->addSP_Constraint(sp5);
theDomain->addSP_Constraint(sp6);
TimeSeries *theSeries = new LinearSeries();
LoadPattern *theLoadPattern = new LoadPattern(1);
theLoadPattern->setTimeSeries(theSeries);
theDomain->addLoadPattern(theLoadPattern);
Vector theLoadValues(2);
theLoadValues(0) = fh * 1.0;
theLoadValues(1) = -50.0;
NodalLoad *theLoad = new NodalLoad(1, 4, theLoadValues);
theDomain->addNodalLoad(theLoad, 1);
AnalysisModel *theModel = new AnalysisModel();
EquiSolnAlgo *theSolnAlgo = new Linear();
StaticIntegrator *theIntegrator = new LoadControl(1.0, 1, 1.0, 1.0);
ConstraintHandler *theHandler = new PenaltyConstraintHandler(1.0e8,1.0e8);
RCM *theRCM = new RCM();
DOF_Numberer *theNumberer = new DOF_Numberer(*theRCM);
BandSPDLinSolver *theSolver = new BandSPDLinLapackSolver();
LinearSOE *theSOE = new BandSPDLinSOE(*theSolver);
StaticAnalysis theAnalysis(*theDomain,
*theHandler,
*theNumberer,
*theModel,
*theSolnAlgo,
*theSOE,
*theIntegrator);
int ok = theAnalysis.analyze(1);
opserr << node4->getDisp();
return ok;
}
int main(int argc, char **argv)
{
for (int fh = 1; fh <= 1000; fh++) {
for (int a1 = 1; a1 <= 10; a1++) {
parametric(fh, a1);
}
}
exit(0);
}
|
这个 main.cpp 文件定义了两个函数,一个用于调用 C++ 的 OpenSees 分析,另一个 main 是程序的入口点,进行参数化。
下面,再建立一个 Makefile ,把 EXAMPLES/Example1 中的 Makefile 复制过来,并加以改动
1
2
3
4
5
6
7
8
9
10
11
| include ../../Makefile.def
PROGRAM = parametric
all: $(PROGRAM)
$(PROGRAM): main.o
$(LINKER) $(LINKFLAGS) main.o ../../SRC/api/elementAPI_Dummy.o \
$(FE_LIBRARY) $(MACHINE_LINKLIBS) \
$(MACHINE_NUMERICAL_LIBS) $(MACHINE_SPECIFIC_LIBS) \
-o $(PROGRAM)
|
可以看到,这里使用了很多变量,大多数是从 ../../Makefile.def 中读取的。也就是在 /home/ops/OpenSees 根目录下的 Makefile.def 文件。这里定义了一些连接文件在哪里找到。
目前根目录下是没有这个 Makefile.def 文件的。因为操作系统不同,有很多种这个文件,放在 MAKES 文件夹里。打开 MAKES 文件夹,我们使用其中的 Makefile.def.EC2-Ubuntu 文件,复制到根目录,并命名为 Makefile.def。
打开这个 Makefile.def 文件,可以看到它的前部有
1
2
3
4
5
6
7
8
9
10
11
12
13
| OpenSees_PROGRAM = $(HOME)/bin/OpenSees
OPERATING_SYSTEM = LINUX
GRAPHICS = NONE
GRAPHIC_FLAG = -D_NOGRAPHICS
PROGRAMMING_MODE = SEQUENTIAL
DEBUG_MODE = NO_DEBUG
RELIABILITY = NO_RELIABILITY
BASE = ./usr/local
HOME = ./home
FE = $(HOME)/OpenSees/SRC
|
这里的 HOME 是存储 OpenSees 的根目录。在这里,我们把这一行替换成
即可。
至此,就可以编译我们刚才写的代码了。首先在 Makefile.def 的注释中,有所依赖的程序的介绍。我们按介绍安装程序包,并建立文件夹。
然后,把原代码编译成库。在 OpenSees 文件夹的根目录中,输入 make libs 。等待编译完成。
然后,进入 EXAMPLES/Parametric 文件夹,输入 make ,即可编译出一个名为 Parametric 的可执行文件。然后通过 ./Parametric 可以运行这个文件。
对于 Linux 系统的配置过程,可以参考我在 DockerHub 维护的 OpenSees docker 镜像的 Dockerfile 。它是从一个只有 5.2M 的最小的 Linux 系统 Alpine 开始,编译 OpenSees 的全过程。这里复制过来。如果对 Docker 不熟悉,可以跳过这一段。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| FROM alpine:3.12
ENV TAG v3.2.0
RUN apk update && apk upgrade && \
apk add sed wget bash make git gcc g++ gfortran tcl=8.6.10-r0 tcl-dev=8.6.10-r0 && \
mkdir /home/ops && \
cd /home/ops && \
mkdir OpenSees bin lib && \
cd OpenSees && \
git init && \
git remote add origin https://github.com/OpenSees/OpenSees.git && \
git config core.sparsecheckout true && \
echo "/SRC" >> .git/info/sparse-checkout && \
echo "/OTHER" >> .git/info/sparse-checkout && \
echo "/Makefile" >> .git/info/sparse-checkout && \
echo "/MAKES/Makefile.def.EC2-UBUNTU" >> .git/info/sparse-checkout && \
echo "/DEVELOPER" >> .git/info/sparse-checkout && \
git pull origin master --tags && \
git checkout $TAG && \
cp MAKES/Makefile.def.EC2-UBUNTU Makefile.def && \
sed -i 's#INTERPRETER_LANGUAGE = PYTHON#INTERPRETER_LANGUAGE = TCL#' Makefile.def && \
sed -i 's#HOME\t\t= ./home#HOME\t\t= /home/ops#' Makefile.def && \
sed -i 's#/usr/lib/x86_64-linux-gnu/libtcl8.6.so#/usr/lib/libtcl8.6.so#' Makefile.def && \
make
WORKDIR /data
ENV PATH $PATH:/home/ops/bin
VOLUME ["/data"]
CMD ["OpenSees"]
|
运行时间比较
三种调用 OpenSees 的方法都介绍完了,下面我们来运行它们。由于 OpenSeesPy 对 MacOS 的支持有问题,我使用的是在多伦多大学办公室的 Windows 电脑中的 Ubuntu WSL2 系统通过 SSH 来运行的。
测试时,为了方便,共运行3次,取3次中的中位数。由于 控制台的 I/O 输出占用时间较长,我们统计一个含输出的时间,再统计一个完全不含输出的时间 (把 puts 等语句去掉)。
| 调用方式 |
用时(无输出) |
用时(有输出) |
| TCL |
0.456 s |
1.178 s |
| Python |
3.653 s |
5.028 s |
| C++ |
0.152 s |
0.998 s |
由此可以看出,使用 C++ 速度最快。在无输出时,使用 TCL 的用时比 C++ 长 200%,而 Python 的用时长 2304%。即使有输出,Python的速度也要远远慢于 TCL,并慢于 C++。
尽管 OpenSees 提供了不同的解释器,但是性能的差异是巨大的。对于简单的模型,可能差别不大,但是如果是参数化分析,例如 Monte Carlo 模拟、敏感性分析等,应该选择速度更快的方法。
这里的讨论仅限于以上简单的线性桁架模型静力分析。它的特点是计算很简单,analyze 语句只执行一次线性分析。但是建模操作相对来讲步骤较多。对于计算复杂的模型,如时程分析等,耗时主要在计算上,性能差异可能就没有这么明显了。在本文中不再过多讨论了。
加快 Python 调用 OpenSees 的速度
Python 调用 OpenSees 的速度很慢,但是 Python 的功能太过强大,是无法被 tcl 取代的。因此,加快 Python 调用 OpenSees 速度就是一个很实际的话题。
对于参数化分析问题,可以把一次分析的模型封装成一个函数,然后通过 Python 来调用这个函数。以此方式,可以减少 Python 的调用次数,加快运行速度。
具体方法,请见加快 Python 调用 OpenSees 的速度。
源码下载
本文与加快 Python 调用 OpenSees 的速度一文的源码可以点此下载。



